√1000以上 多 角形 の 求め 方 209646-直角三角形 角度 ��め方 中学生
学研教育情報資料センター 算数 学習相談 小/算数/5年/量と測定/ 四角形・三角形の面積/理解シート 五角形(多角形)の面積を求めるには,どうすればいいの 無断複製・転載・翻訳を禁ず GAKKENB 正n角形の面積も、 「周りの長さ 高さ÷2」 で求められることがわかります。 ここで、円の面積について考えましょう。 正n角形の辺の数(nの値)を極限まで増やすと、円になります。 つまり、正n角形の面積の公式が使えます。 すると、円の面積は正多角形の角度は「180 (n-2)/n」で算定します。 nは正多角形の角度の数です。 なお、「180 (n-2)」は正多角形の内角の和を求める式です。 前述の公式を使えば簡単に正多角形の角度が算定できます。 例えば、正四角形の1つの角度は「180× (4-2)÷4=360÷4=90°」です。 また内角の和=180× (4-2)=360°ですね。 今回は、正多角形の角度の値と計算式、正6角形、正9
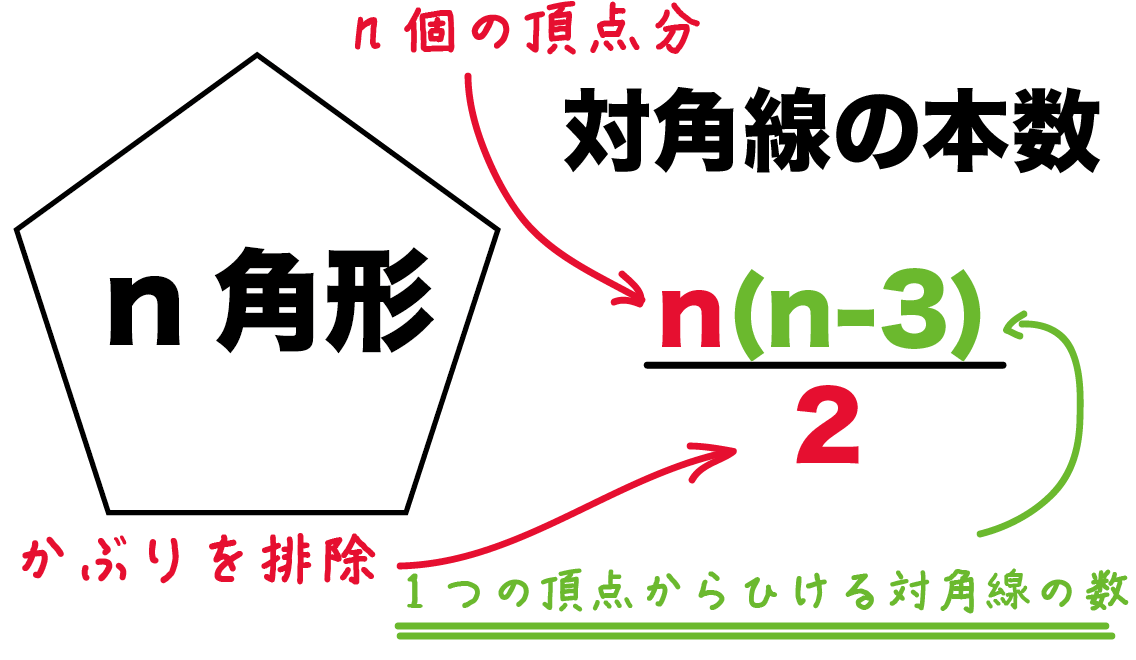
簡単公式 多角形の対角線の本数が5秒でわかる求め方 Qikeru 学びを楽しくわかりやすく
直角三角形 角度 求め方 中学生
直角三角形 角度 求め方 中学生- 面積公式 多角形の面積は、頂点の位置ベクトルから 外積 を用いて計算することができる。 多角形の頂点を反時計回りに並べて、それらの位置ベクトルを とすると、その面積は という式になる。 ただし、 とする。 この式を使うと凹多角形でも問題動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru




多角形の内角の和の公式と外角の和を利用した角度の求め方
Mathematics 國中 約3小時以前 ・ この正多角形の求め方教えてください🙇♀️ 9 1つの内角が108°である正多角形は何か。 0 解答 奏音 約2小時以前 2種類方法があるので2つご紹介します (求める正多角形をn角形とします) ① 内角の和=180 (n2多角形の内角の和・外角の和の公式 多角形の内角の和と外角の和の公式をまとめると以下の通り。 N角形の内角の和:180°× (N −2) 180 ° × ( N − 2 ) 多角形の外角の和:360° 360 ° 内角の和は三角形の180°から、角が増えるごとに180°ずつ増えていき 東大卒講師歴年の図解講師「そうちゃ」が公式で求められない四角形の面積を求め方をまとめました。記事を真似して問題をとけば、たいていの問題は解けるよ 東大卒講師歴年の図解講師による そうちゃ式 受験算数(2号館 図形/速さ) ホーム 平面図形基礎 中学受験求積の工夫。
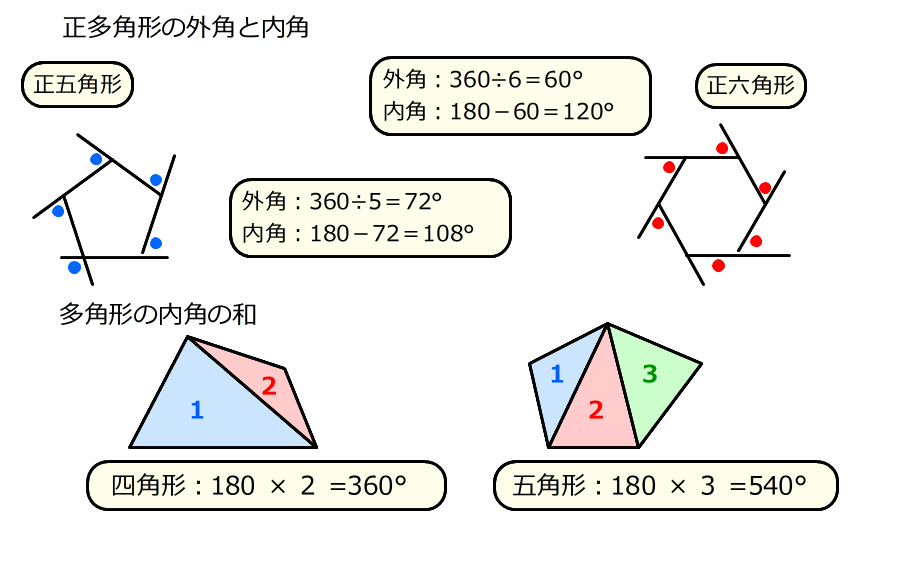
多角形 問題の解き方を教えてください🙇 3 正七角形の1つの内角(右 の図中の ∠x) の大きさを 求めなさい。 X 多角形 0 解答 最佳解答 アカギ 5分鐘以前 解き方⑴ 正十角形の内角の和は 180×(102)=1440度 よって1つの内角の大きさは 1440÷10=144度 解き方⑵ 正十角形の1つの外角の大 公式の導出方法 正多角形の面積導出には、sinで表す三角形の面積公式\(\frac{1}{2}\sin{\theta}ab\)を使用します この公式の導出についてはこちらの記事で解説していますので、興味のある方は是非ご覧ください sinで表す三角形の面積公式と導出方法よって、多角形の内角の和の公式より、正多角形の一つ一つの内角は$$\frac{180°×(n2)}{n}$$と求めることができます。 また、正多角形における外角もすべて等しいため、正多角形の一つ一つの外角も$$\frac{360°}{n}$$と、 和の公式を $n$ で割る ことで求められます。
正多角形の場合の数 場合の数と確率 正多角形の対角線の数、正多角形の頂点で作る三角形についての場合の数を考えます。 正八角形ぐらいまでなら手書きで考えられるかもしれませんが、それ以上になると手書きでは難しいと思います。 一般化して正n角形で考えてみることで、どの正多角形についても答えられるようになるでしょう。 目次 対角線の個数 辺を共有する三角形の個数 直角三角形の個 多角形の性質(角度や面積を求める)解き方と問題一覧 単元別の研究 ※<予習シリーズ解説サンプルページ> 右の図の平行四辺形の面積は何cm2ですか。 (1)右の図の三角形の底辺は13cmで,面積は52cm2です。高さは何mですか。 (2)右の台形の下底は8cm,高さは6cmで,面積は33cm2ご意見・ご感想 直径27センチの円形テーブルに置ける正方形のレンジパンの一片の長さを計算するのにとても役立ちました。 最初にある円が不完全だったのか、数ミリ誤差が生まれた。 万華鏡の筒に内接する正多角形の一辺を計算で求めたかった
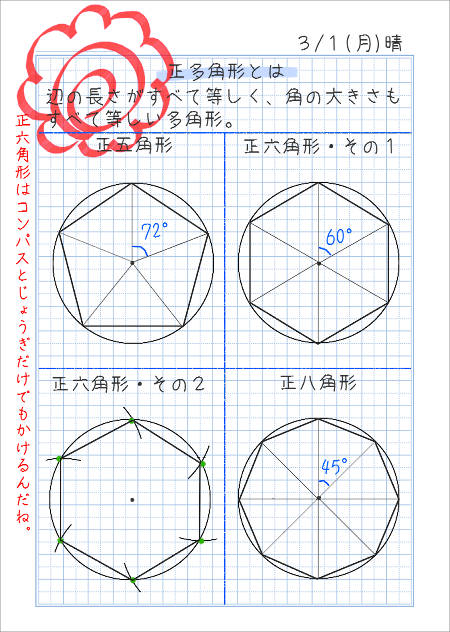



いろいろな正多角形をかいてみよう 家庭学習レシピ
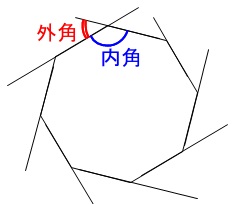



多角形の内角の和の公式と外角の和を利用した角度の求め方
多角形の面積の求め方は、多角形を対角線で三角形に分けて、それぞれの三角形の面積を加える。 図の中の垂直な2本の直線が、三角形の底辺と高さになるように分ける。 多角形の面積を求める問題の解説 斜線部分の面積を直接求めることはできないので、 補助線をひき、 3つの三角形㋐ 引用元 予習シリーズ算数 4年下 第3回「円と正多角形」練習問題より(四谷大塚出版) ほぼフリーハンドで書きましたので残念ながら正九角形にはなりませんでした。 まあそれはいいでしょう。 (1)は楽勝ですね。 (9ー2)×180÷9=140 答え 140° 正多角形の一つの内角の大きさを求める公式は↓でしたね。多角形 問題の解き方を教えてください🙇 3 正七角形の1つの内角(右 の図中の ∠x) の大きさを 求めなさい。 X 多角形 0 回答 まだ回答がありません。 回答するにはログインが必要です。 ログインして質問に回答する 新規登録 疑問は解決しましたか? 解決した 解決しなかった
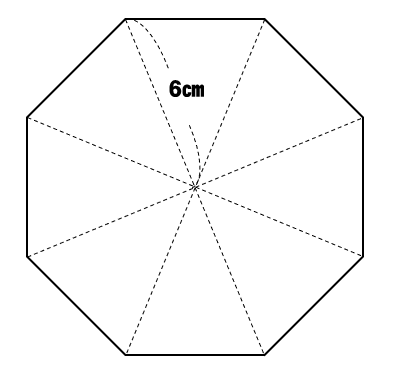



中学数学 正八角形の面積を三平方の定理で求める方法を解説 数スタ




多角形の外角の求め方を5分でサクッと理解 中学数学 理科の学習まとめサイト
正多角形の面積 中学入試の答えを知るため。 (02角形の対角線の本数) sqrt (xx) のように指定してください。 正多角形の1番長い対角線の長さを表示してほしい。 1辺を1としたときと仮定した時でいいので。 非常に役に立った。 立式できても計算に辺の長さ(a) 30 2 辺の数(n) 5 3 周囲(l) =b1*b2 4 角度(θ) =180*(12/b2) 5 対角線の数(m) =(b2*(b23))/2 6 面積(s) =(b2*b1^2)/(4*tan(pi()/b2))多角形の内角の和の公式 \(\color{red}{180^{\circ}\times (n2)}\) を覚えているのなら、当然ですが正多角形にも使えるので \(\hspace{10pt}180^{\circ}\times (92)\\ =1260^{\circ}\) でも、もちろん良いです。 または外角の和がいつも\(\,360°\,\)であることから、 正九角形の外角の1つは



内角の和 180 N 2 外角の和 360 教遊者



1
多角形を用いた求め方 3<π<4の証明 の流れを汲んで π π の値を求めることを考える。 基本的には の不等式に基づいて多角形の角の数を多くすることで π π を上下から挟みこむ方針である。 実はこの不等式は「周」を「面積」としても n n に依存する 図1のように、赤い4角形各辺の垂直二等分線が円に交わる点を新たな頂点として追加すれば青い8角形が得られ, 同様に各辺の垂直二等分線によって緑の16角形が得られ、以下同様に 32角形, 64角形 を作図することができます。 正多角形とは、すべての辺、角の大きさが等しい多角形のことをいいます。 つまり、 正多角形の1つ分の内角は、内角の和を等分することで求めれます。 例 (正三角形) 内角の和180° ⇒ 1つ分の内角\(180\div3=\color{red}{60°}\) (正六角形)




5年算数 正多角形と円 正六角形について調べよう Youtube



多角形とは 外角 内角の和 面積 対角線の公式と求め方 受験辞典
多角形の性質(角度や面積を求める)解き方と問題一覧 ※お知らせ 5年下 解説の発売を開始しました。 7/25 (月) スケジュールにそって掲載をしていきます。 ※<サイト内はコチラからお入りください> 右の図の平行四辺形の面積は何cm2ですか。 (1)右の内角の和を考える方法 それぞれの方法について解説していきます。 外角を利用する方法 内角と外角って 多角形の面積の求め方算数からやさしく解説 多角形の面積 面積とはざっくりと言うと、(主に平らな)図形の大きさ(広さ)を表す量のことです。 多角形には三角形や四角形はもちろん、五角形、六角形、\ 算数・物理・数学トピック
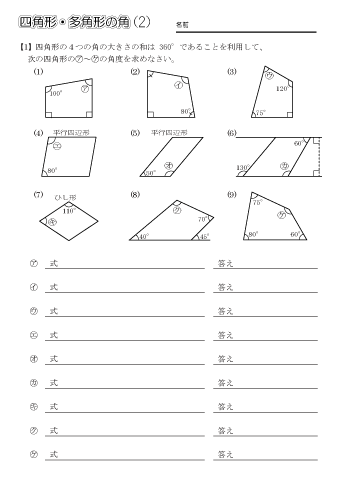



小学5年生の算数 四角形 多角形の角 問題プリント ちびむすドリル 小学生




多角形の角度の和の求め方 添付画像の黒い印の角の角度の和を求めたいのです Okwave
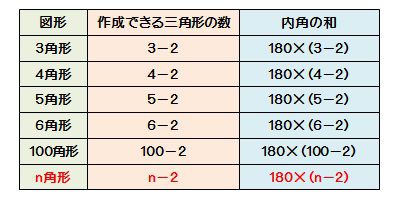
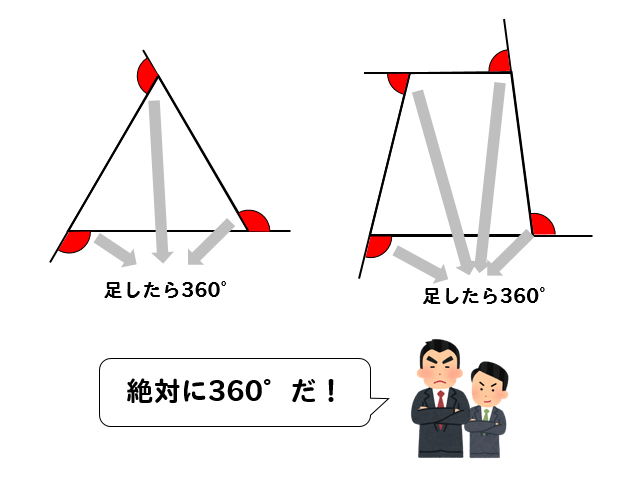
隣り合う内角と外角の和は180° まず1つ目は、 外角の和は常に360°になる ということです。 三角形だろうが、六角形だろうが、百角形だろうが! どんな多角形であっても外角を全部集めて足すと360°になります。 次は、 隣り合う内角と外角の和は180°になる ということです。 「隣り合っている=直線になっている」 ってことだから、足したら180°になる 多角形の面積の求め方の活用例 多角形の面積をそのままの形で求めようとすると難しいですが、今回の三角形などのより簡単なものを使って分割して考えることで問題を解決することは数学ではもちろんのこと生活の中でも活用できます。 社会やビジネスがよりわかる!数字に強くなるN角形の内角の和=180×(n-2) この公式を忘れてしまったらどうしたらよいでしょうか? 多角形の内角の和は求められないでしょうか? そんなことはありません。 忘れてしまった場合は、前項で使用したこんな表を自分で作成してみましょう。 三角形
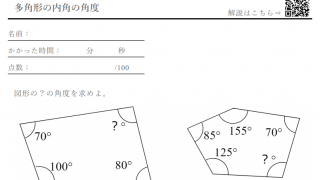



多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun
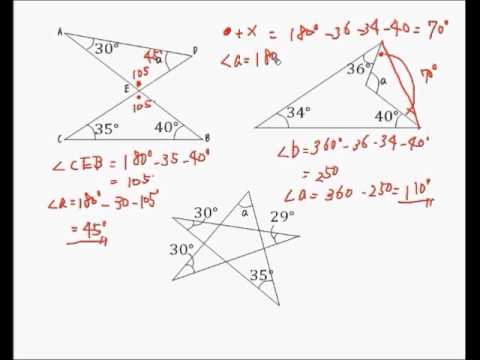



多角形から角を求める Youtube
この正多角形の求め方教えてください🙇♀️ 9 1つの内角が108°である正多角形は何か。 0 回答 まだ回答がありません。 回答するにはログインが必要です。 ログインして質問に回答する 新規登録 疑問は解決しましたか? 解決した 解決しなかった この質問を見ている人は こちらの質問も 中学2年生数学の 「多角形の内角と外角」学習プリント・練習問題 です。 三角形の角 の特徴を理解したあとは、多角形の角の特徴について学習しましょう。 多角形の内角の和や外角の和を求める問題を出題しています。 内角の和や外角の和が求められる 各三角形の乗じた結果を合計し全面積で割ると図形全体の重心座標が算出できます。 以下の入力フォームに座標のリストを入力して計算ボタンをクリックすると重心及び面積を算出します。 また座標から図形を表示します。 表には算出過程の値が表示さ




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学




小5 算数 小5 54 正多角形 Youtube
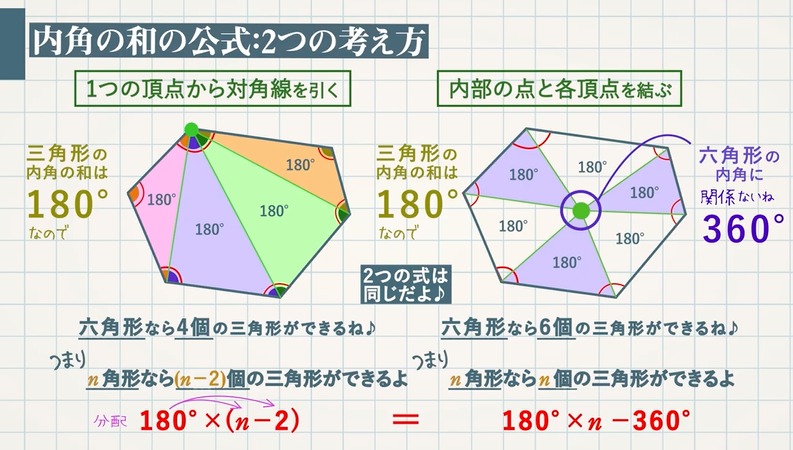
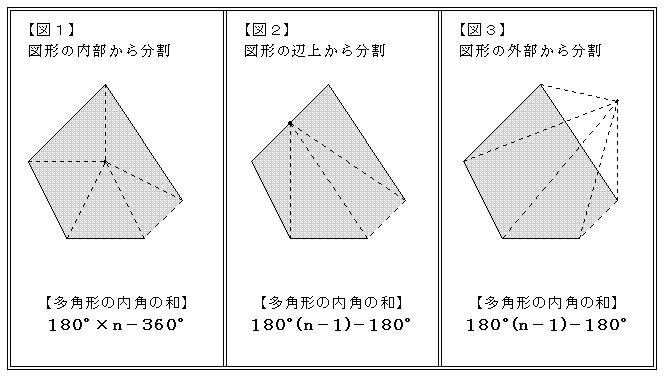
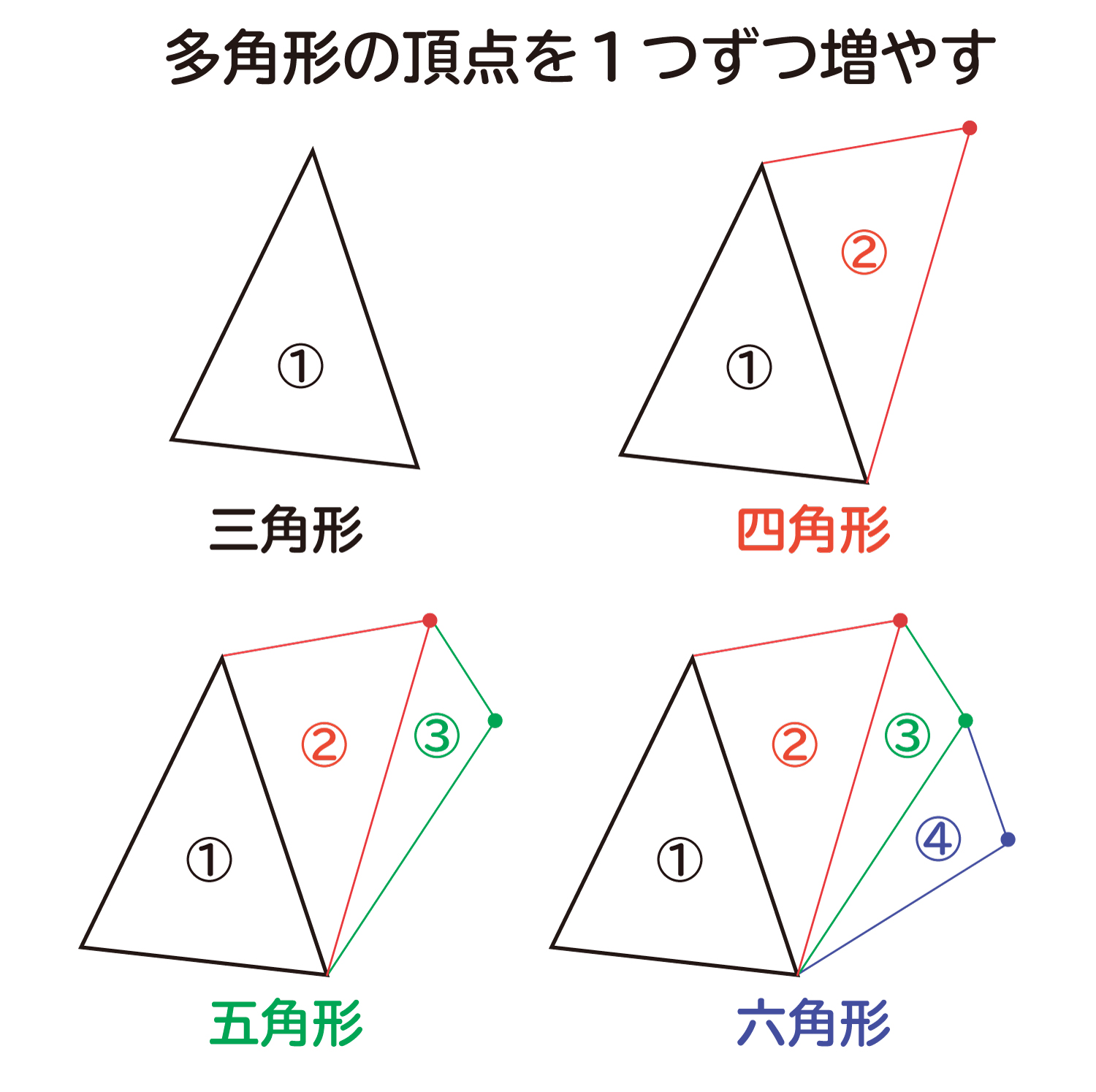
五角形より角の多い多角形でも、角が1つ増えるごとに、分けられる三角形の数は1つずつ増えていきます。 これを式にしてまとめると、 「n角形の内角の和は180°× (n-2)」 となります。 ぴよ校長 n角形は、(n-2)個の三角形に分けることができるよ! 例)九角形の場合は、n=9なので、九角形の内角の和は180°× (92)=180°×7=1260° まとめ ・ 多角形は角が1つ増える



正8角形です あ い う それぞれの角度の求め方を教えてください 一つの角の Yahoo 知恵袋




多角形の内角の和 算数の公式覚えてますか




面積 面積の求め方のくふう 01 面積の公式を使って Youtube




多角形の内角の和 は何度なのか を説明します おかわりドリル
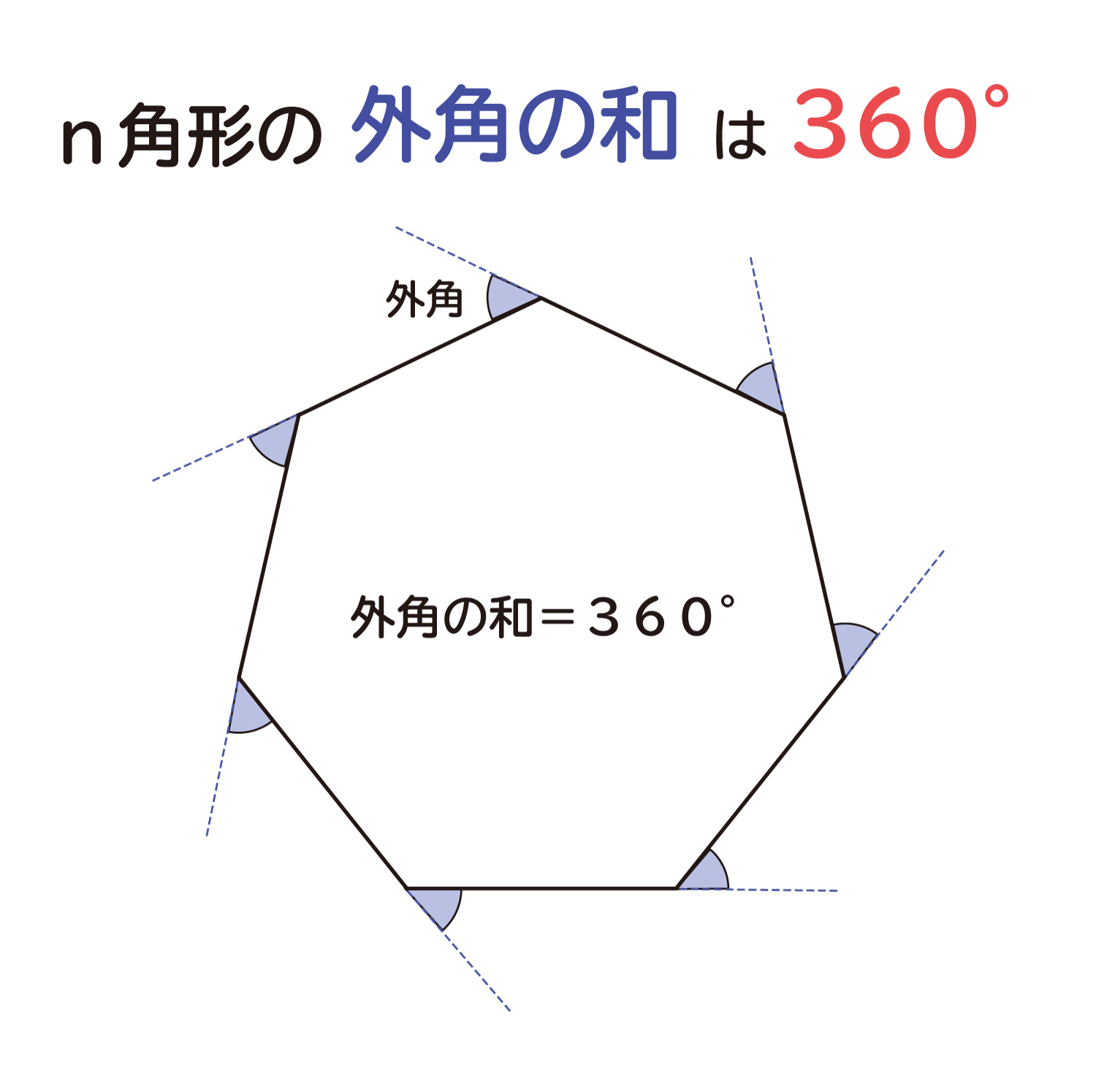



なぜ n角形の外角の和は360 なのか を説明します おかわりドリル



多角形の重心座標計算



多角形の内角の和 算数の公式覚えてますか




内角の和から多角形を求める方法と一覧表 具体例で学ぶ数学




内角の和 180 N 2 外角の和 360 教遊者




多角形の内角の和 外角の和の公式 数学fun
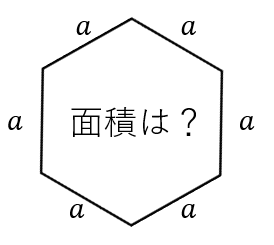



正六角形の面積 計算ツール 公式の導出 具体例で学ぶ数学




正多角形を定規だけで描く 交点座標から線で結ぶ方法 Alumania Information




高校数学 正多角形の面積の求め方 例題編 映像授業のtry It トライイット
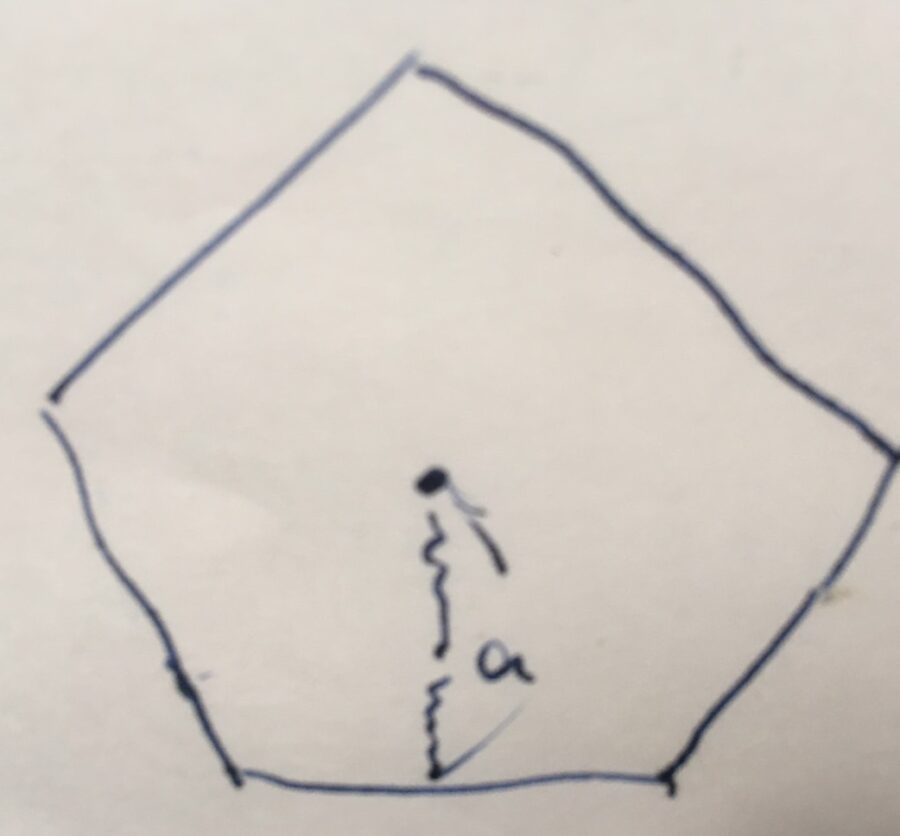



正多角形の面積の求め方 証明 趣味の大学数学




小学校5年 算数 正多角形の角の大きさ Youtube




多角形の内角の和 算数の公式覚えてますか




つくばサイエンスエッジ18 文京学院大学女子高校 みらいぶ 高校生サイト



3 多角形の重心




3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ



多角形の面積を求める Javascript版
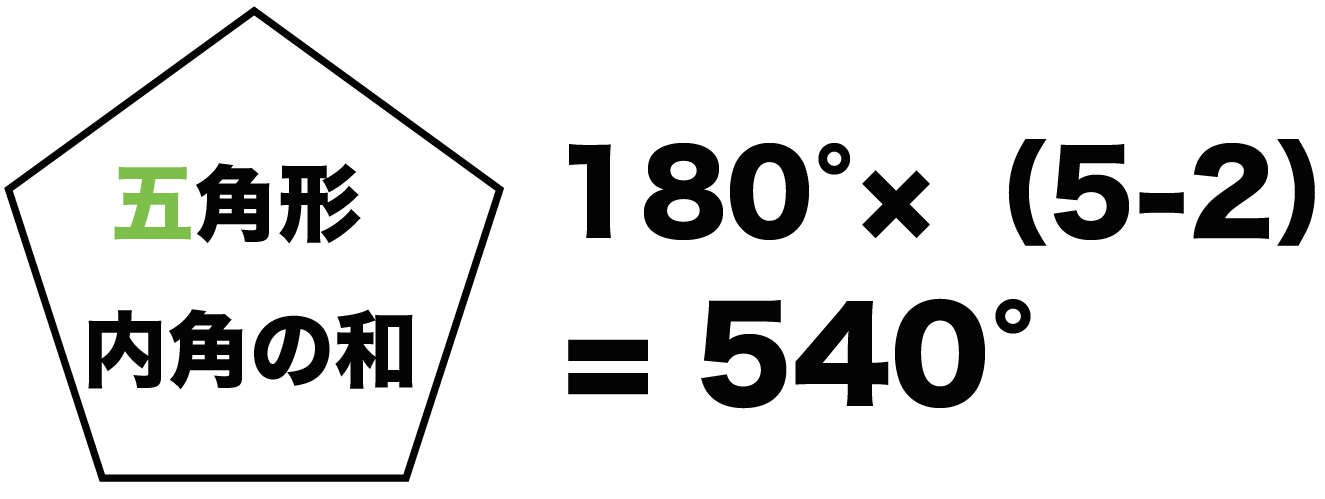



中2数学 多角形の内角の和が3秒でわかる公式 Qikeru 学びを楽しくわかりやすく



三平方の定理から円周率を計算してみる Yamav1 02bのブログ



正 多 角形 の 内角 の 和 簡単公式 五角形の内角の和を3秒で計算できる方法 Stg Origin Aegpresents Com



正六角形 正6角形 の角度の求め方は 1分でわかる値 内角の和 外角 正多角形の角度の求め方



多角形の対角線の本数を求める公式 具体例で学ぶ数学




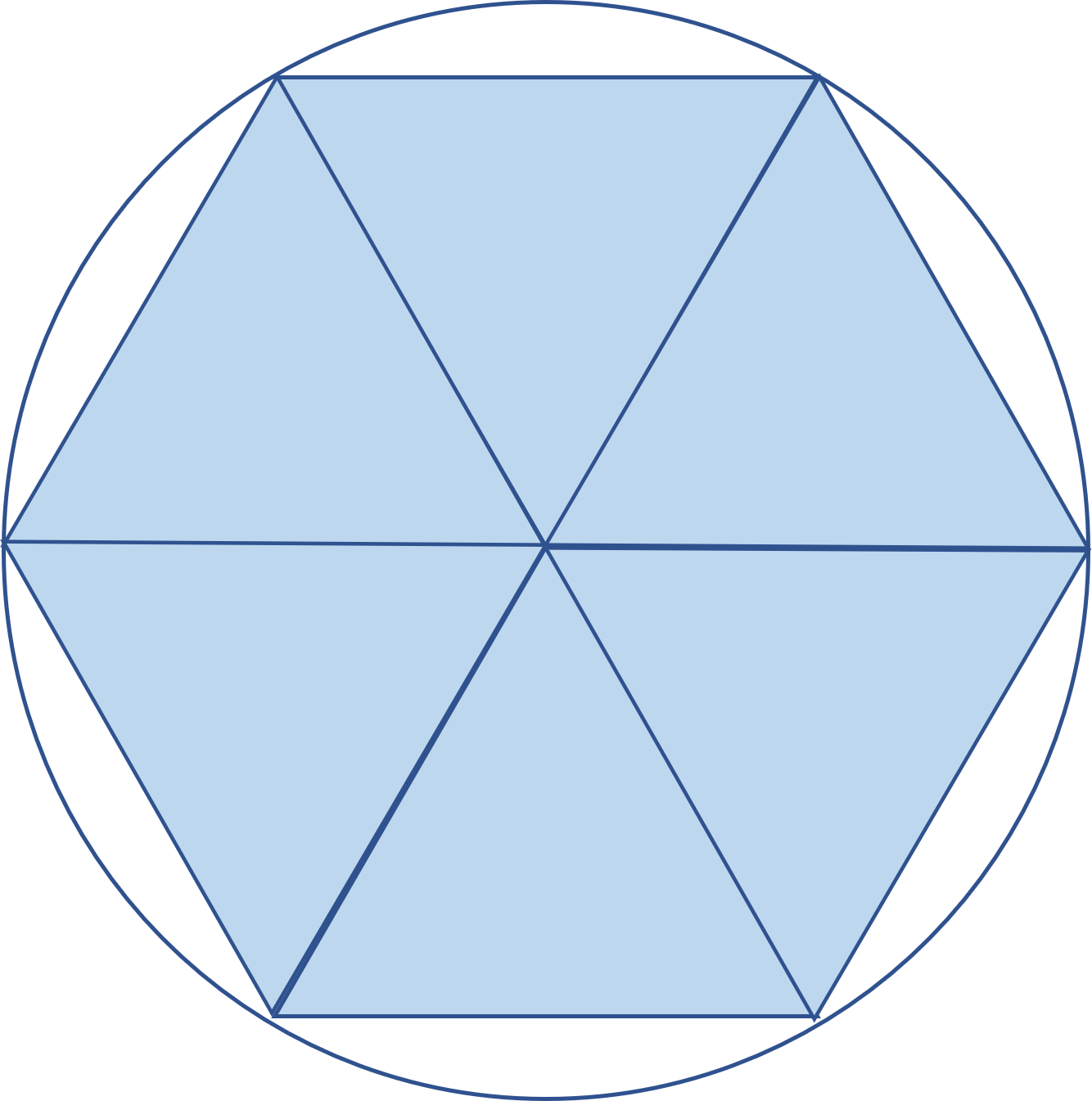
正多角形の面積から円の面積の公式へ 算数を究める




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学



5年算数 正多角形と円周の長さ わかる教え方



多角形の面積の求め方 算数からやさしく解説 数学 統計教室の和から株式会社




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun



小5算数 正多角形と円 指導アイデア みんなの教育技術




課題学習の指導 数学




正 多 角形 の 内角 の 和 簡単公式 五角形の内角の和を3秒で計算できる方法 Stg Origin Aegpresents Com




高校数学 正多角形の面積の求め方 練習編 映像授業のtry It トライイット




高校数学 正多角形の面積の求め方 映像授業のtry It トライイット



3 多角形の重心



1




中2数学 正多角形の外角の大きさが3秒でわかる公式 Qikeru 学びを楽しくわかりやすく
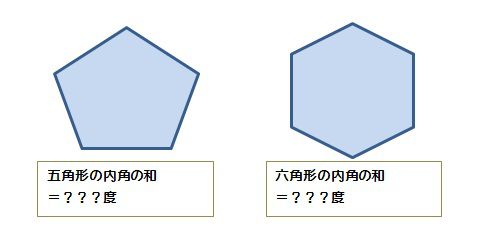



多角形の内角の和 算数の公式覚えてますか




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun
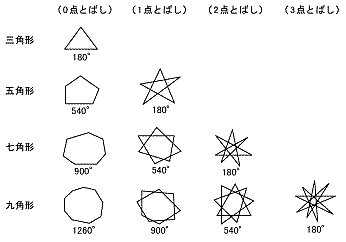



課題学習の指導 数学
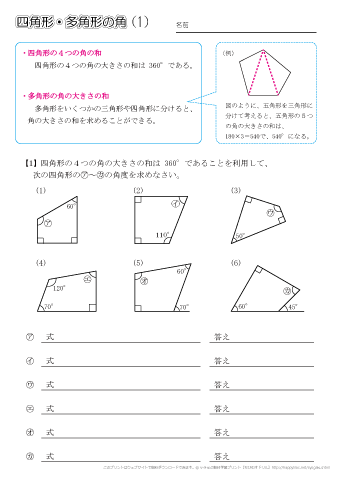



小学5年生の算数 四角形 多角形の角 問題プリント ちびむすドリル 小学生




正多角形の1つの内角 外角を求める方法を問題解説 数スタ
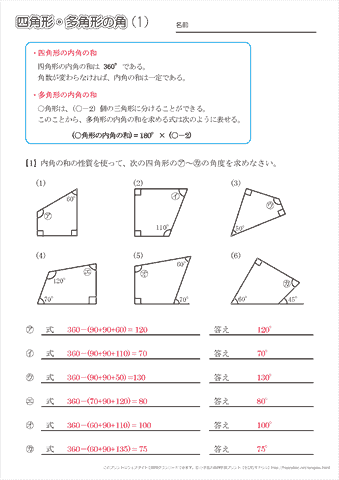



小学5年生の算数 四角形 多角形の角 問題プリント ちびむすドリル 小学生




多角形の面積の求め方 算数からやさしく解説 数学 統計教室の和から株式会社
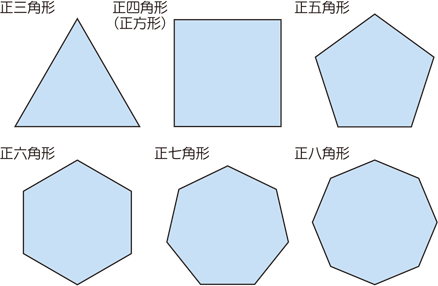



正多角形 算数用語集
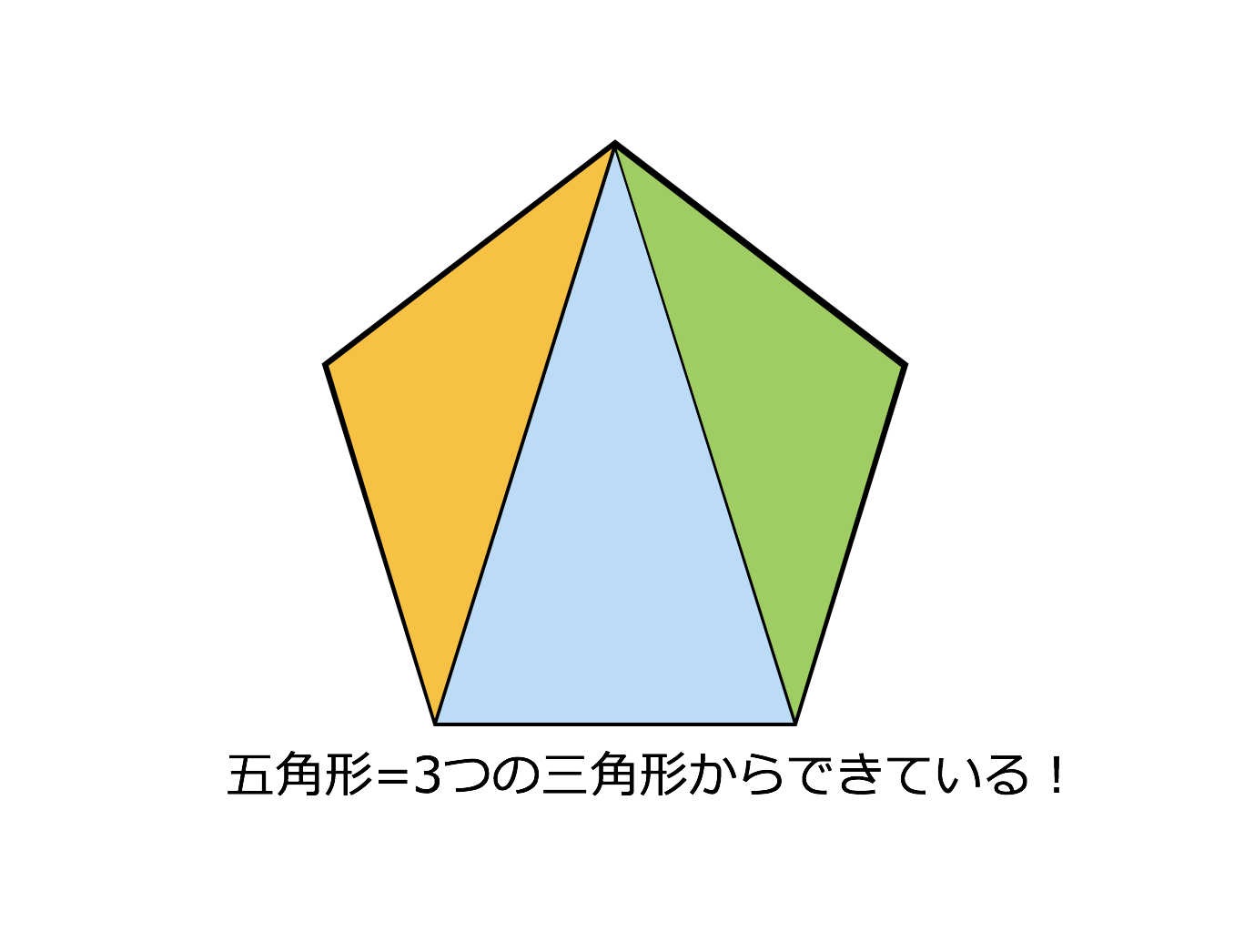



3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ




Math 対角線の数から 多角形が何角形かを求める問題 働きアリ




正 多 角形 の 内角 の 和 簡単公式 五角形の内角の和を3秒で計算できる方法 Stg Origin Aegpresents Com




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学
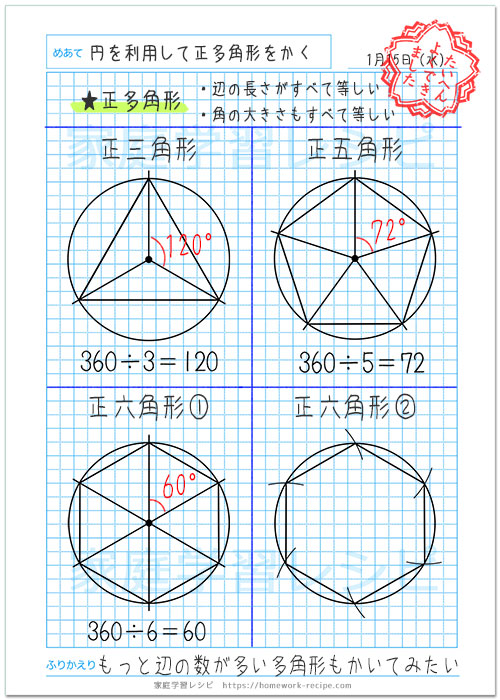



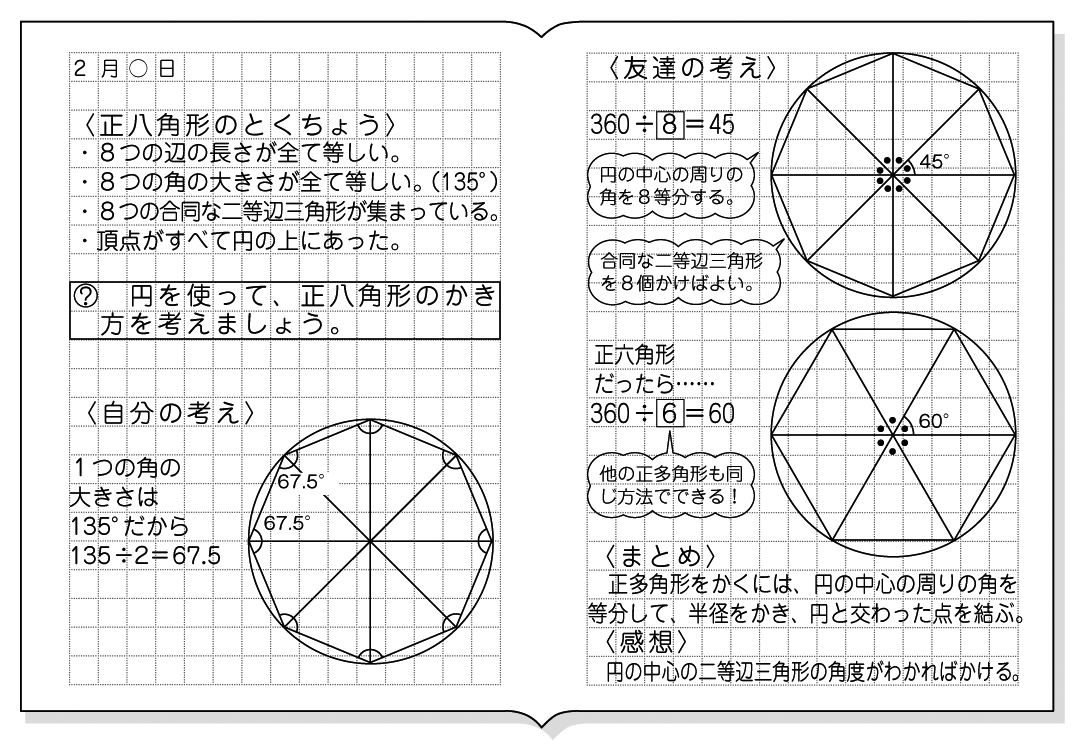
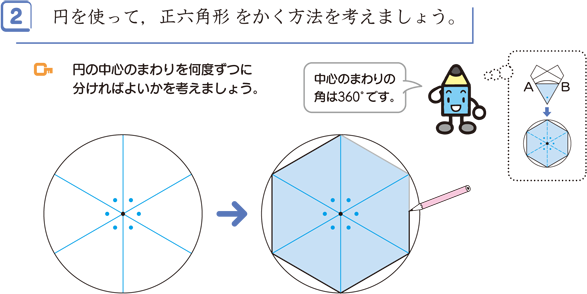
円を利用して正多角形をかく方法 算数の自主学習 家庭学習レシピ



多角形とは 外角 内角の和 面積 対角線の公式と求め方 受験辞典
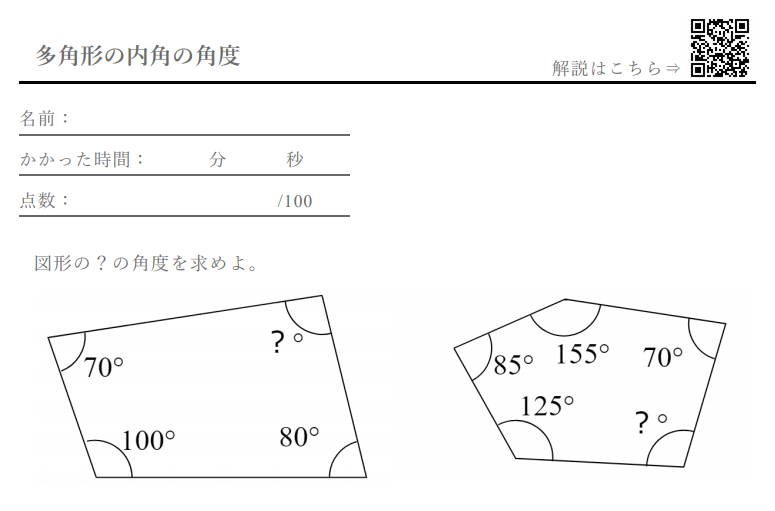



多角形 の内角の角度 計算ドリル 問題集 数学fun



小5 算数 小5 33 多角形の角 Youtube
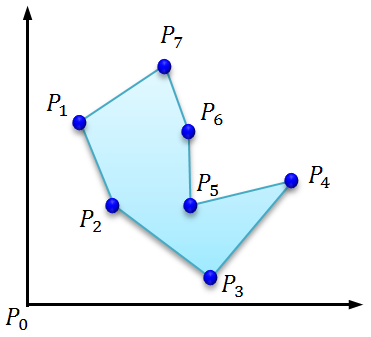



N点からなる多角形の面積を求める イメージングソリューション




簡単公式 多角形の対角線の本数が5秒でわかる求め方 Qikeru 学びを楽しくわかりやすく




内角の和 180 N 2 外角の和 360 教遊者




数学 中2 51 多角形の内角と外角の和 基本編 Youtube




正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく
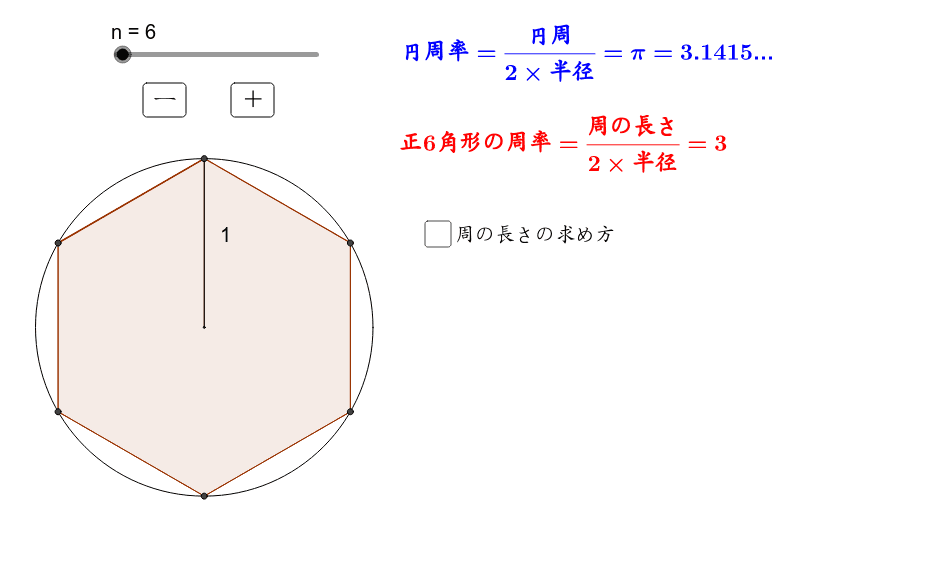



円周率と正多角形 Geogebra




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun




中学受験 対角線の数は 公式を忘れなくする論理的3ステップ かるび勉強部屋
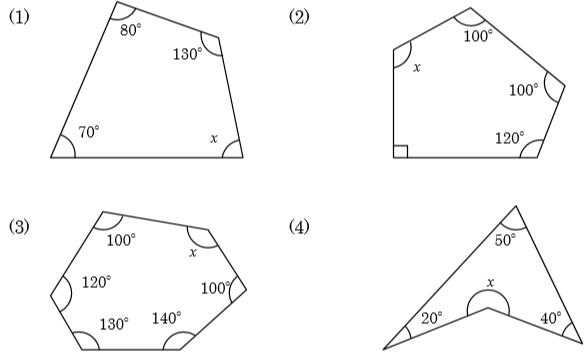



中2数学 多角形の内角の和と外角の和のポイントと練習問題 Pikuu



正多角形の1つの内角 外角を求める方法を問題解説 数スタ



多角形の面積で円周率を求める Allisone



多角形の面積
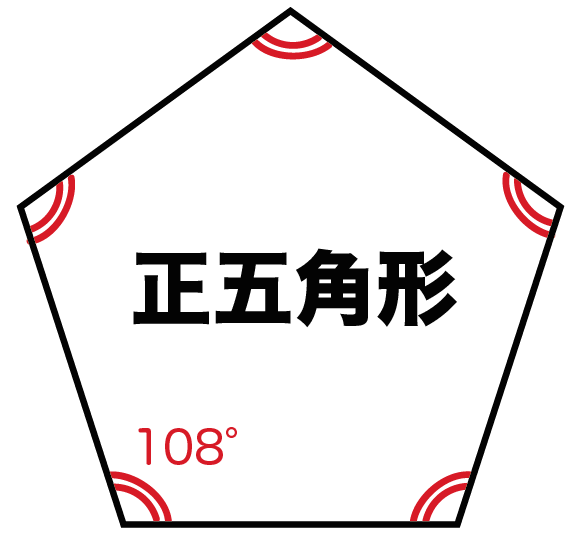



正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく



正多角形 Wikipedia



正 多 角形 の 内角 の 和 簡単公式 五角形の内角の和を3秒で計算できる方法 Stg Origin Aegpresents Com



正 多 角形 の 内角 の 和 簡単公式 五角形の内角の和を3秒で計算できる方法 Stg Origin Aegpresents Com




中2数学 正多角形の外角の大きさが3秒でわかる公式 Qikeru 学びを楽しくわかりやすく



正多角形 算数用語集



多角形の角



正8角形 正八角形 の角度の求め方は 1分でわかる内角の和 計算 外角 正9角形の角度




正多角形の対角線の長さ 香料ゐっすゐの夢



3




多角形の内角の和の公式と外角の和を利用した角度の求め方
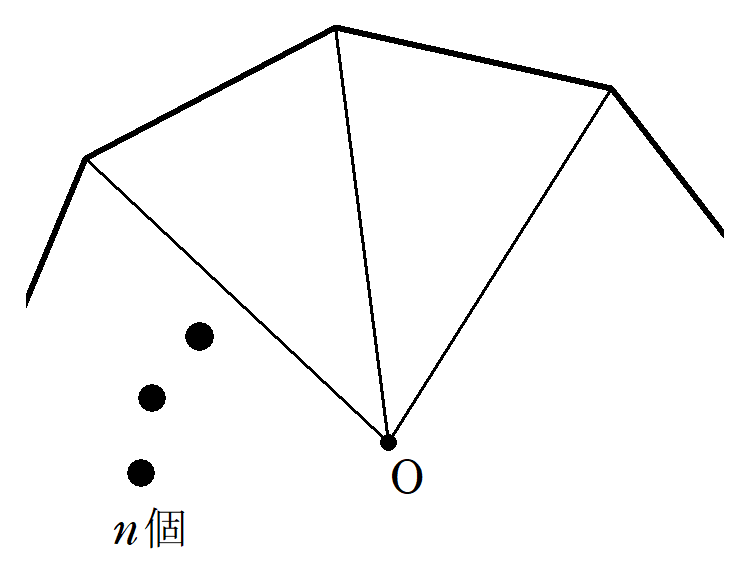



正多角形の面積の公式 一辺 A の正 N 角形の面積は1つの式で表せる Fukusukeの数学めも
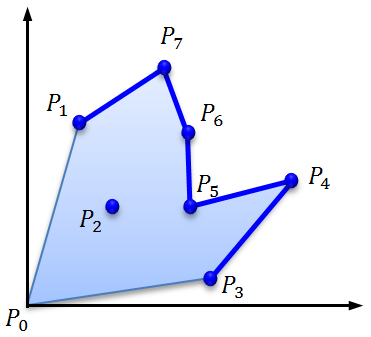



N点からなる多角形の面積を求める イメージングソリューション



正 多 角形 の 内角 の 和 簡単公式 五角形の内角の和を3秒で計算できる方法 Stg Origin Aegpresents Com
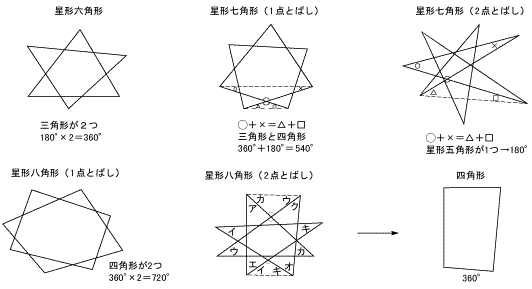



課題学習の指導 数学



3




内角の和の公式 内角の和が1800 の多角形は何角形 中学や高校の数学の計算問題




多角形の内角の和 は何度なのか を説明します おかわりドリル




内角の和 180 N 2 外角の和 360 教遊者




外角の求め方 外角の和を使って多角形の角度を求める問題 中学や高校の数学の計算問題
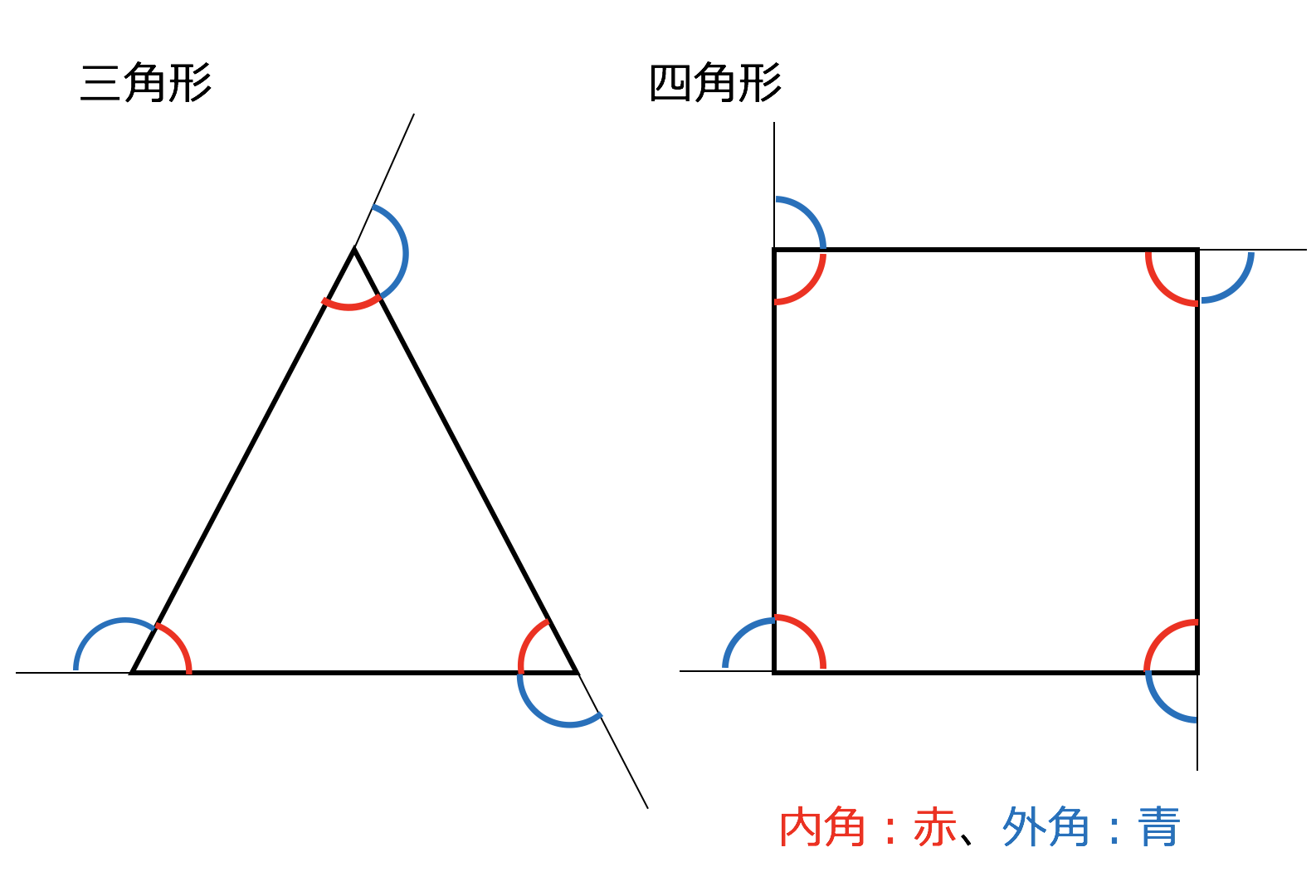



3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ




正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学
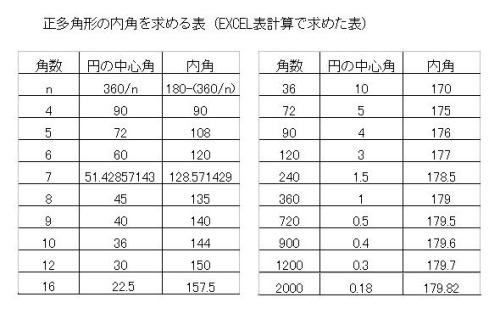



正多角形の角数を大きく増加して行くとその内角は180度に近づく 多面体紙工作で数学を楽しむ 行動の記録 楽天ブログ
コメント
コメントを投稿